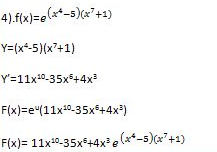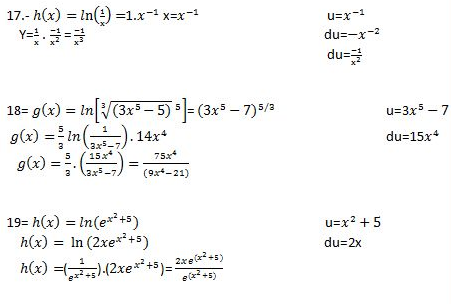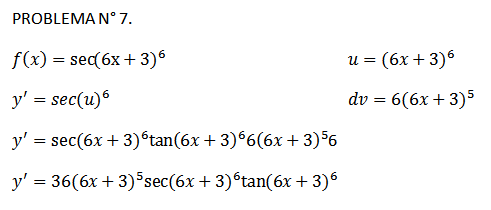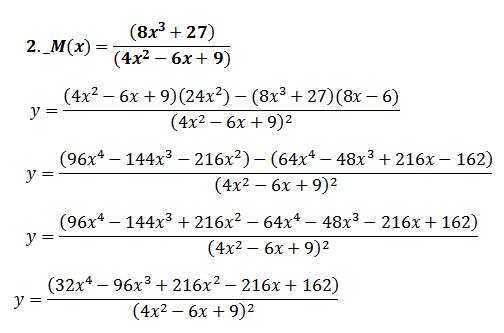REGLA DE LA CADENA
En cálculo, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones.
Descripción de la regla
En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser computado como el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
Descripción algebraica
En términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si F es diferenciable en X y g es una función diferenciable en f(x), entonces la función compuesta (g o f) (x) = g (g(f(x)) es diferenciable en X y
(g o f)(x)= d (g o f) / dx = d g (f(x))/dx = d/dx g(f(x)) = g (f(x)) .f(x)
Notación de Leibniz
Alternativamente, en la notación de Leibniz, la regla de la cadena puede expresarse como:
dg/dx = dx/df df/dx
donde dg/df indica que g depende de f como si ésta fuera una variable.
REGLA DE LA CADENA DERIVADAS